本文共 2914 字，大约阅读时间需要 9 分钟。

解法1 – 暴力出奇迹

穷举出所有可能的连续子序列，并计算出它们的和，最后取它们中的最大值

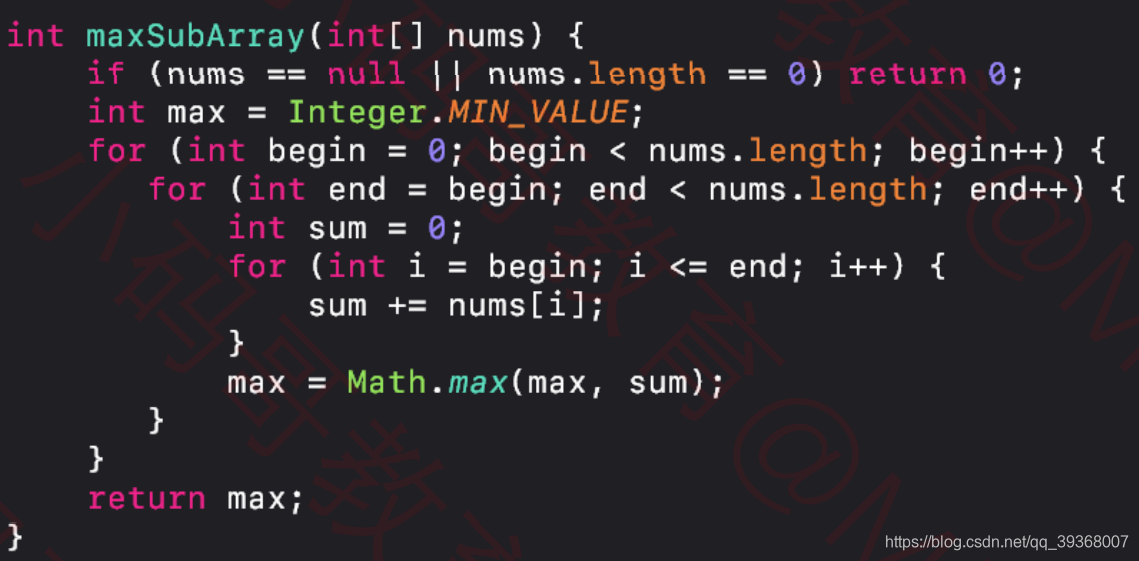
空间复杂度：O(1)，时间复杂度：O （n 3）

class Solution {    public int maxSubArray(int[] nums) {        if (nums == null || nums.length == 0) return 0;        int max = Integer.MIN_VALUE;        for (int begin = 0; begin < nums.length; begin++) {            for (int end = begin; end < nums.length; end++) {                // sum是[begin, end]的和                int sum = 0;                for (int i = begin; i <= end; i++) {                    sum += nums[i];                }                max = Math.max(max, sum);            }        }           return max;    }}

所以，需要对此进行改进

重复利用前面计算过的结果

空间复杂度：O(1)，时间复杂度：O （n 2）

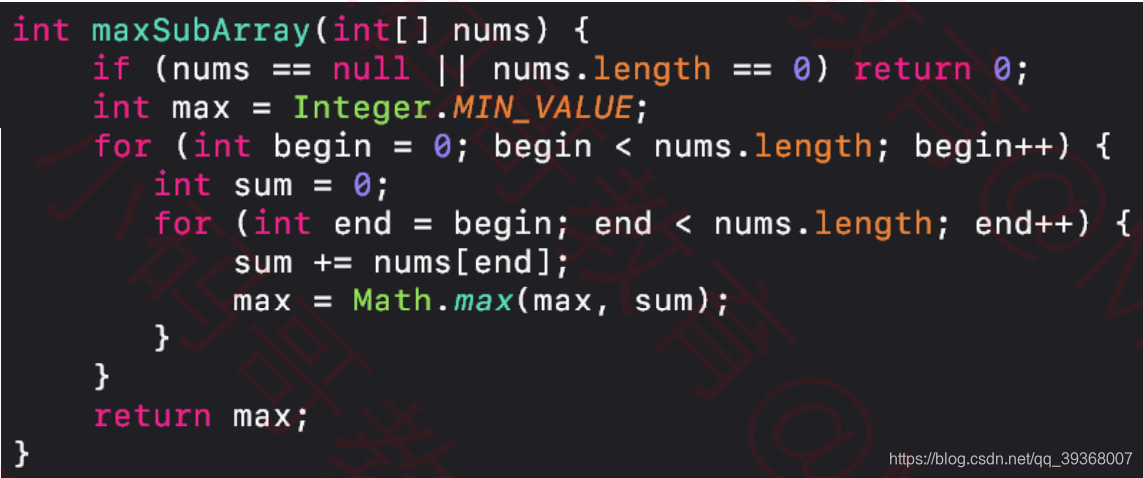
class Solution {    public int maxSubArray(int[] nums) {        if (nums == null || nums.length == 0) return 0;        int max = Integer.MIN_VALUE;        for (int begin = 0; begin < nums.length; begin++) {            int sum = 0;            for (int end = begin; end < nums.length; end++) {                // sum是[begin, end]的和                sum += nums[end];                max = Math.max(max, sum);            }        }        return max;    }}

解法2 – 分治

class Solution {   public int maxSubArray(int[] nums) {        if (nums == null || nums.length == 0) return 0;        return maxSubArray(nums, 0, nums.length);    }    static int maxSubArray(int[] nums, int begin, int end) {        if (end - begin < 2) return nums[begin];        int mid = (begin + end) >> 1;        int leftMax = Integer.MIN_VALUE;        int leftSum = 0;        for (int i = mid - 1; i >= begin; i--) {            leftSum += nums[i];            leftMax = Math.max(leftMax, leftSum);        }        int rightMax = Integer.MIN_VALUE;        int rightSum = 0;        for (int i = mid; i < end; i++) {            rightSum += nums[i];            rightMax = Math.max(rightMax, rightSum);        }        return Math.max(leftMax + rightMax,                Math.max(                        maxSubArray(nums, begin, mid),                        maxSubArray(nums, mid, end))        );    }}

class Solution {   public int maxSubArray(int[] nums) {        if (nums == null || nums.length == 0) return 0;        return maxSubArray(nums, 0, nums.length);    }    static int maxSubArray(int[] nums, int begin, int end) {        if (end - begin < 2) return nums[begin];        int mid = (begin + end) >> 1;        int leftMax = nums[mid - 1];        int leftSum = leftMax;        for (int i = mid - 2; i >= begin; i--) {            leftSum += nums[i];            leftMax = Math.max(leftMax, leftSum);        }        int rightMax = nums[mid];        int rightSum = rightMax;        for (int i = mid + 1; i < end; i++) {            rightSum += nums[i];            rightMax = Math.max(rightMax, rightSum);        }        return Math.max(leftMax + rightMax,                Math.max(                        maxSubArray(nums, begin, mid),                        maxSubArray(nums, mid, end))        );    }}

转载地址：http://loznz.baihongyu.com/